Geometrie-Výpočty
Skleněné těžítko CERMAT M9-24-PAD - 2

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 2

Skleněné těžítko má tvar rotačního válce s poloměrem podstavy 10 cm a výškou 12 cm. Vnější část těžítka je z čirého skla, uvnitř je část z modrého skla, která má také tvar rotačního válce, a to s poloměrem podstavy 5 cm a výškou 8 cm.

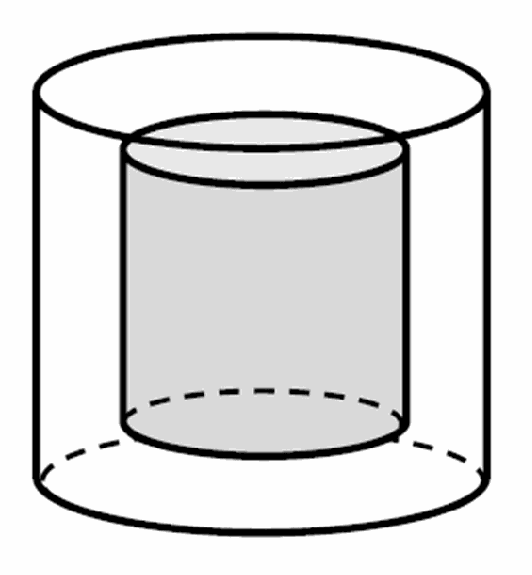
Vypočítejte objem čirého skla v těžítku.

Výsledek zaokrouhlete na desítky cm³. Pro výpočet použijte zaokrouhlenou hodnotu čísla

π ≐ 3, 14

.

Řešení:

Správná odpověď:

3140 cm3

Postup:

Matěj Zelenka

Čiré sklo obklopuje vnitřní válec z modrého skla, jeho objem tudíž vypočítáme odečtením objemu modrého skla od objemu celého tělesa.

Výpočet objemu celého válcového těžítka:

\begin{array}{r} V_{c} = S_{p c} \cdot v_{c} = π \cdot r_{c}^{2} \cdot v_{c} = π \cdot 10^{2} \cdot 12 = 1200 π \end{array}

Geometrie-VýpočtyPředchozíSkleněné těžítko CERMAT M9-24-PAD - 2Další

Řešení:

Geometrie-Výpočty
Skleněné těžítko CERMAT M9-24-PAD - 2