Geometrie-Výpočty
CERMAT M9-24-PCD - 6

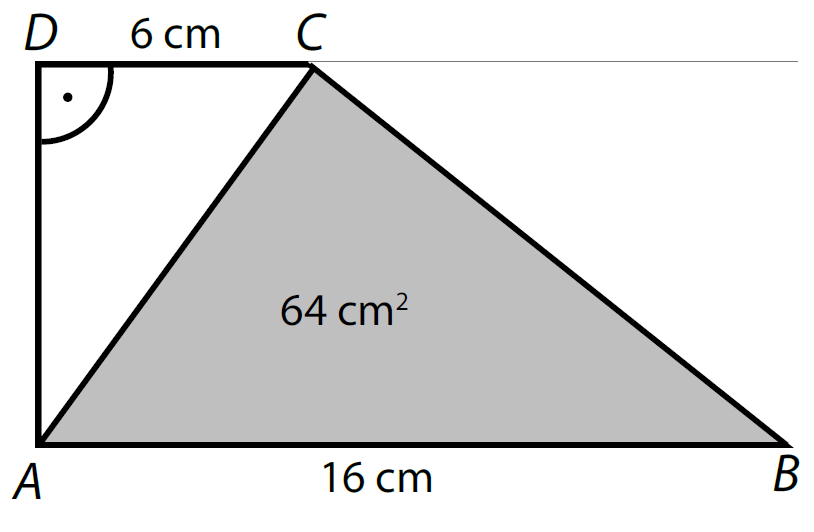
Pravoúhlý lichoběžník ABCD se základnami AB a CD a s pravým úhlem při vrcholu D je úhlopříčkou AC rozdělen na dva trojúhelníky ABC a ACD.

Pro délky stran platí: |AB| = 16 cm, |CD| = 6 cm. Obsah trojúhelníku ABC je 64 cm².

6.1 Vypočítejte výšku lichoběžníku ABCD.

Výsledek uveďte v cm.

6.2 Vypočítejte obsah lichoběžníku ABCD.

Výsledek uveďte v cm².

Řešení:

Správná odpověď:

8 cm
88 cm2

Postup:

Adam Demeter6.1 Pro výpočet výšky trojúhelníku použijeme vzorec $ S= \frac{ v\cdot c}{2}$, kde S je objem, v je výška a c je strana
$$
64=\frac{ 16\cdot v}{2}
$$
šestnáctka se vykrátí s dvojkou
$$
64=8\cdot v
$$
celé to vydělíme osmi
$$
x=8
$$

výsledek je: $ 8 cm $

Adam Demeter6.2 K výpočtu obsahu budeme potřebovat výšku lichoběžníku z úlohu 6.1. Tenhle postup to bude počítat přes vzorec obsahu lichoběžníku.
Vzorec pro výpočet obsahu pravoúhlého lichoběžníku je $ S = \frac{ (a+c)\cdot v }{2}$, kde V je obsah, a, c jsou strany lichoběžníku a v je výška
$$
S = \frac{ ( 16+6 )\cdot 8}{2}
$$
nejprve se zbavíme závorky a osmičku vykrátíme s dvojkou
$$
S = 22\cdot 4 = 88
$$

výsledek je: $ 88cm^{ 2}$

Adam Demeter6.2 K výpočtu obsahu budeme potřebovat výšku lichoběžníku z úlohu 6.1. Tenhle postup bude sčítat obsahy trojuhelníků.
jeden z obsahů už je vypočítaný a pro výpočet druhého použijeme vzoreček $ S=\frac{ v\cdot c}{2}$, kde S je obsah, v je výška a c je strana trojúhelníku
$$
S_{ 1}=\frac{ 8\cdot 6}{2}
$$
osmička se vynásobí s šestkou a vydělíme to dvěma
$$
S_{ 1}=\frac{ 48}{2} = 24
$$
Teď stačí sečíst obsahy obou trojúhelníků $ S=S_{ 1}+S_{ 2}$

$$
S=64+24 = 88
$$

výsledek je: $ 88cm^{ 2}$

Komentáře/hodnocení

Geometrie-VýpočtyPředchozí CERMAT M9-24-PCD - 6Další

Řešení:

Postup:

Geometrie-Výpočty
CERMAT M9-24-PCD - 6