m
Předchozí CERMAT M9-25-PAD - 7Další

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 7
V rovině leží přímky p, q, r, které se protínají v bodě R,
a přímky s, t, pro které platí: s ∥ r, s ⊥ t.
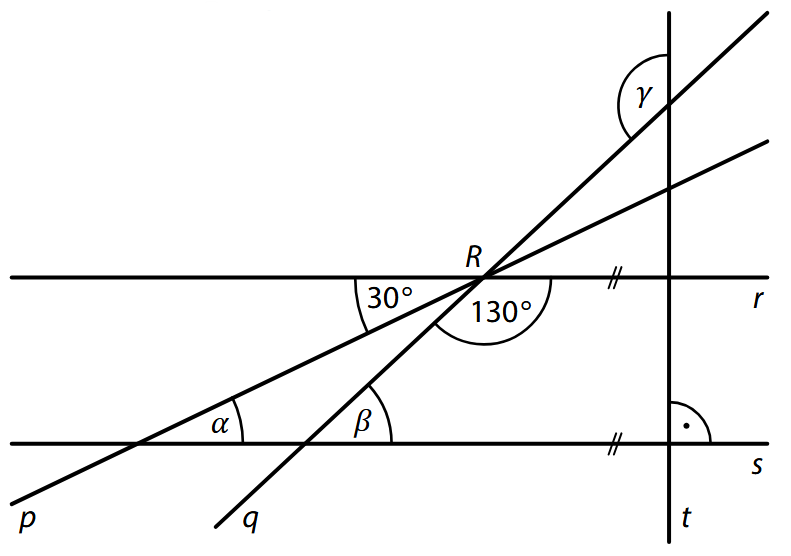(CZVV)

Vypočtěte ve stupních velikost úhlu
7.1 \( \alpha \),
7.2 \( \beta \),
7.3 \( \gamma \).

Velikosti úhlů neměřte, ale vypočtěte (obrázek je pouze ilustrativní).

Řešení:

Správná odpověď:

30°;50°;140°

Postup:

Matěj Zelenka

Vypočtěte ve stupních velikost úhlu
7.1 \( \alpha \):
Díky rovnoběžnosti přímek s a r platí, že úhel svíraný přímkami p a s je shodný jako ten svíraný p a r. Nazíváme je úhly souhlasné. Takto:Nyní můžeme využít vrcholových (protilehlých) uhlů. Ty jsou také shodné.
$$
\alpha = \underline{\underline{30°}}
$$

7.2 \( \beta \):
I tady využijeme souhlasných a vrcholových úhlů a vidíme, že úhel \( \beta \) je vlastně doplněk 130° do přímého úhlu 180°.Stačí odečíst 130° od 180°:
$$
\beta = 180°- 130° = \underline{\underline{50°}}
$$

7.3 \( \gamma \):
Nyní si vytvoříme rovnoběžku s přímkou s. Nazvěme ji třeba u.

Díky rovnoběžnosti s s je zárověn kolmá na t. Úhel \( \gamma \) můžeme vypočítat jako součet úhlů \( \beta \) a práveho úhlu 90°.
$$
\gamma = \beta + 90° = 50° + 90° = \underline{\underline{140°}}
$$

Výsledek je: 30°; 50°; 140°