m
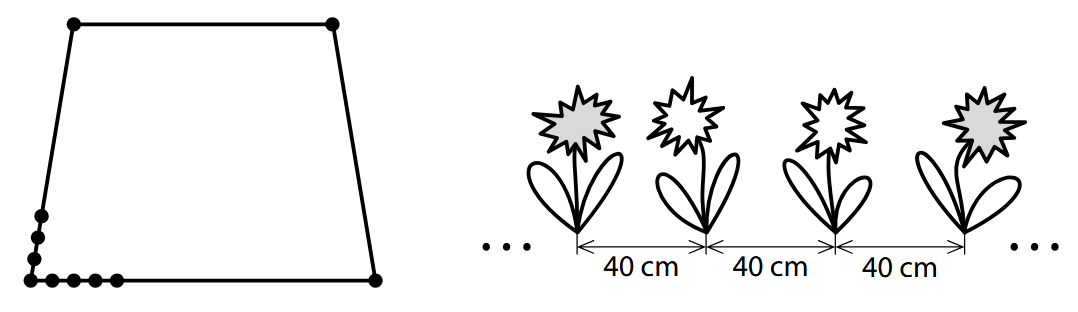
CERMAT M9-25-PAD - 8

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8
Záhon v parku má tvar čtyřúhelníku, jehož tři strany jsou stejně dlouhé. Každá z těchto tří stran je o čtvrtinu kratší, než je čtvrtá strana čtyřúhelníku.
Po obvodu záhonu je ve stejných rozestupech vysázeno celkem 65 rostlin, z nichž je po jedné rostlině i v každém rohu záhonu. Rozestupy mezi rostlinami měří 40 cm.

8.1 Vypočtěte v metrech obvod záhonu.

8.2 Určete, o kolik se liší počet rostlin na nejdelší straně záhonu od počtu rostlin na protější straně záhonu.

8.3 Po obvodu záhonu se pravidelně střídají stejně početné skupinky červeně kvetoucích rostlin s dvojicemi bíle kvetoucích rostlin.
Určete nejmenší možný počet červeně kvetoucích rostlin po obvodu záhonu.

Řešení:

Správná odpověď:

26 m;o 5 rostlin;39 červeně kvetoucích rostlin

Postup:

Matěj Zelenka8.1 Vypočtěte v metrech obvod záhonu.

V zadání je řečeno, že po obvodu záhonu je ve stejných 40cm rozestupech vysázeno celkem 65 rostlin. Stačí nám vynásobit počet rostlin a jejich rozestupy:
$$
65 \cdot 40 = 2600 cm = \underline{\underline{26 m}}
$$

8.2 Určete, o kolik se liší počet rostlin na nejdelší straně záhonu od počtu rostlin na protější straně záhonu.

To, že je každá ze tří stran o čtvrtinu kratší, než poslední čtvrtá strana, můžeme matematicky zapsat tak, že delší strana má $ 1 $ délkovou jednotku a kratší stana má $\frac{ 3 }{ 4 }$ délkové jednotky.
Abychom něměli zbytečně zlomky vynásobíme obě čtyřmi. Delší strana má $ 4 $ části a kratší stana má $ 3 $ části.
Celý obvod (tři kratší a jedna delší stana) má $3+3+3+4=13$ částí, mezi které musíme květiny rovnoměrně rozdělit:
$$
65\colon 13 = 5
$$
To znamená, že na každé naší části je 5 rostlin.

Nejdelší strana má o jednu část více než protější ($ 4 \text{ a } 3 $) a proto má přesně $\underline{\underline{\text{o } 5 \text{ rostlin}}}$ více.

8.3 Po obvodu záhonu se pravidelně střídají stejně početné skupinky červeně kvetoucích rostlin s dvojicemi bíle kvetoucích rostlin.
Určete nejmenší možný počet červeně kvetoucích rostlin po obvodu záhonu.

To, že se pravidelně střídají stejně početné skupinky červeně kvetoucích rostlin s dvojicemi bíle kvetoucích rostlin znamená, že máme vždy sled několika červených rostlin a dvě bílé a zase několik červených rostlin a dvě bílé... Aby platilo, že se pravidelně střídají, musí jejich počet být celočíselný. To pro nás znamená, že celkový počet květin musí být dělitelný počtem květin v každém sledu.
Navíc každý sled nusí mít několik červených a dvě bílé, takže nejméně tři rostliny.
Tady je asi nejjednodušší zkoušet postupně celočíselné dělitele čísla 65:
3 - (6+5=11) ne
4 - také ne
5 - Ano, to je nejmenší celočíselný dělitel 65.

Takže celkem 5 rostlin tzn. že červených je 3 z 5 tedy $ \frac{3}{5} $.

A teď spočítáme nejmenší možný počet červeně kvetoucích. $ \frac{3}{5} $ z celkového počtu 65 rostlin:
$$
\frac{3}{5} \cdot 65 = \underline{\underline{39}}
$$

Komentáře/hodnocení

mPředchozí CERMAT M9-25-PAD - 8Další

Řešení:

Postup:

m
CERMAT M9-25-PAD - 8